How to derive the formula for moment of inertia of a disc about an axis passing through its


Moment of Inertia Simple Definition, Formulas, Examples

This page contains the video Moment of Inertia of a Disc. Browse Course Material Syllabus About the Team Online Textbook Readings. Lesson 29: Moment of Inertia [29.1-29.6] Lesson 30: Torque [30.1-30.5] Lesson 31: Rotational Dynamics [31.1-31.7] Week 10 Worked Example.


The moment of inertia of a circular disc of radius r and mass m about any one of its diameter is

Moment of inertia, denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, it is the rotational analogue to mass. Thin, solid disk of radius r and mass m. This is a special case of the solid cylinder, with h = 0.


The moment of inertia of a uniform semicircular disc of mass M and radius r about a line

The moment of inertia of a thin circular disk is the same as that for a solid cylinder of any length, but it deserves special consideration because it is often used as an element for building up the moment of inertia expression for other geometries, such as the sphere or the cylinder about an end diameter. The moment of inertia about a diameter.


Moment of Inertia of a Disk with a Hole Part 2 YouTube

The moment of inertia is the quantitative measure of rotational inertia, just as in translational motion, and mass is the quantitative measure of linear inertia—that is, the more massive an object is, the more inertia it has, and the greater is its resistance to change in linear velocity. Similarly, the greater the moment of inertia of a.


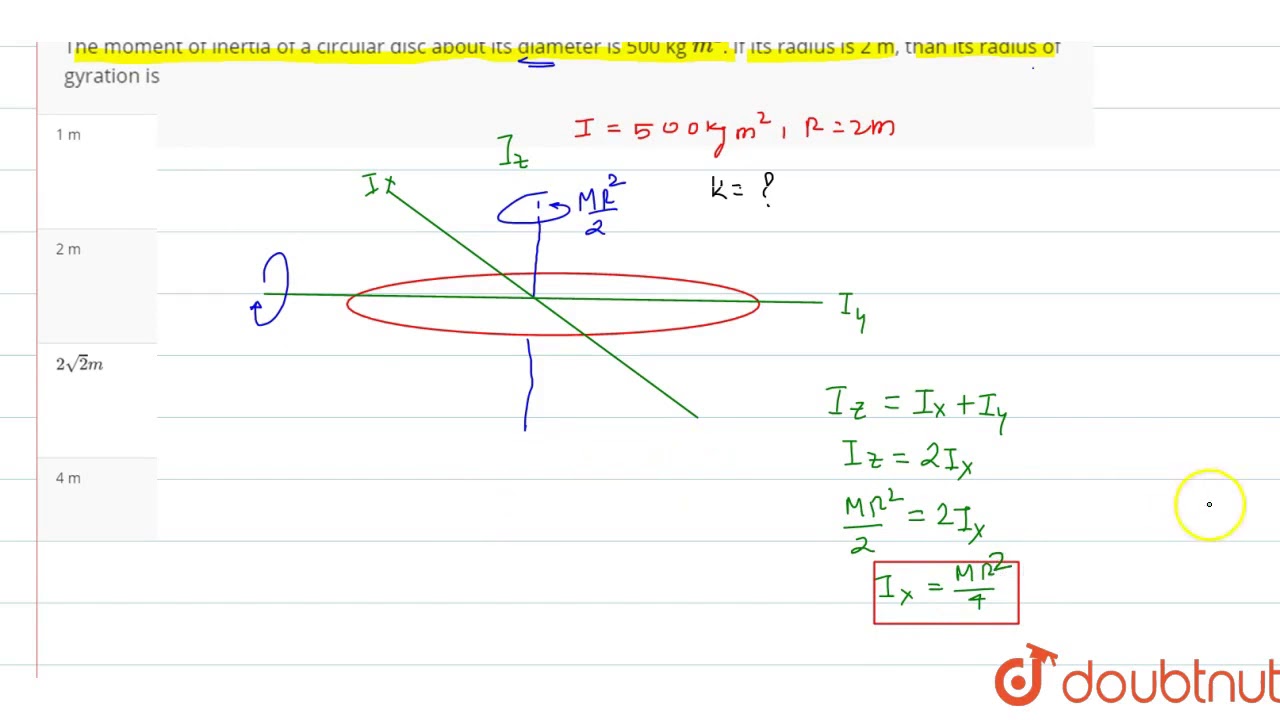
The moment of inertia of a circular disc about its diameter is 500 kg `m^(2)`. If its radius is

The moment of inertia of a solid disk about this axis is given in Figure to be \[\dfrac{1}{2}MR^2,\] where \(M = 50.0 \, kg\) and \(R = 1.50 \, m\), so that. moment of inertia mass times the square of perpendicular distance from the rotation axis; for a point mass, it is I=mr2 and, because any object can be built up from a collection of.


Rotationl dynamic lecture_12./Moment of inertia of a disc YouTube

The moment of inertia of the rod is simply \(\frac{1}{3} m_rL^2\), but we have to use the parallel-axis theorem to find the moment of inertia of the disk about the axis shown. The moment of inertia of the disk about its center is \(\frac{1}{2} m_dR^2\) and we apply the parallel-axis theorem (Equation \ref{10.20}) to find


The moment of inertia of a thin uniform circular disc about one of its diameter is l. Its moment

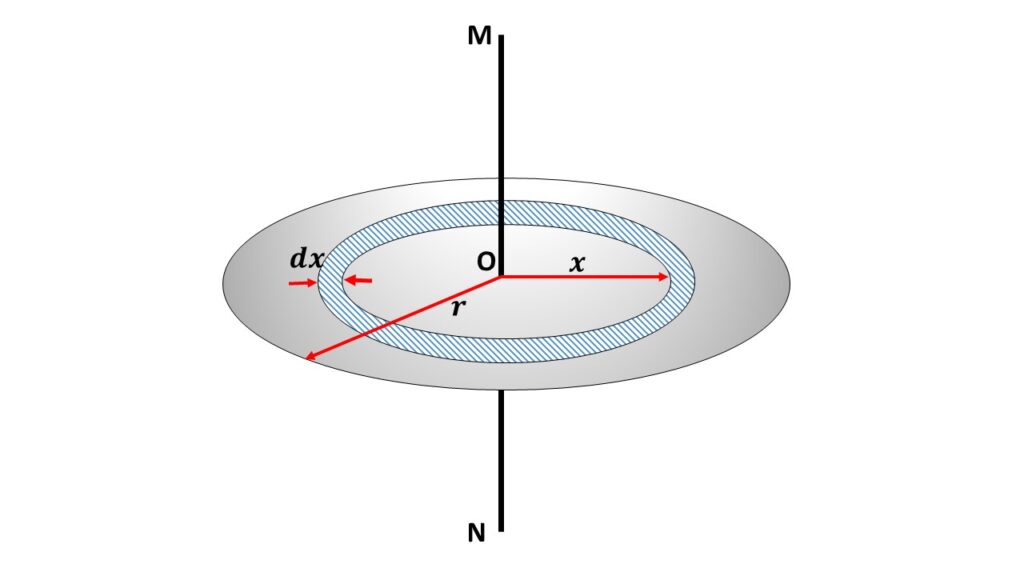
The boxed quantity is the result of the inside integral times dx, and can be interpreted as the differential moment of inertia of a vertical strip about the x axis. This is consistent our previous result. The vertical strip has a base of dx and a height of h, so its moment of inertia by (10.2.2) is. dIx = h3 3 dx.


The movement of inertia of a circular disc of radius 2 m and mass 2 kg , about an axis passing

Rotational inertia is a property of any object which can be rotated. It is a scalar value which tells us how difficult it is to change the rotational velocity of the object around a given rotational axis. Rotational inertia plays a similar role in rotational mechanics to mass in linear mechanics. Indeed, the rotational inertia of an object.


Moment of Inertia of Circular Disk kamaldheeriya YouTube

The moment of inertia of the compound pendulum is now obtained by adding the moment of inertia of the rod and the disc around the pivot point as, =, + +, + (+), where is the length of the pendulum. Notice that the parallel axis theorem is used to shift the moment of inertia from the center of mass to the pivot point of the pendulum.


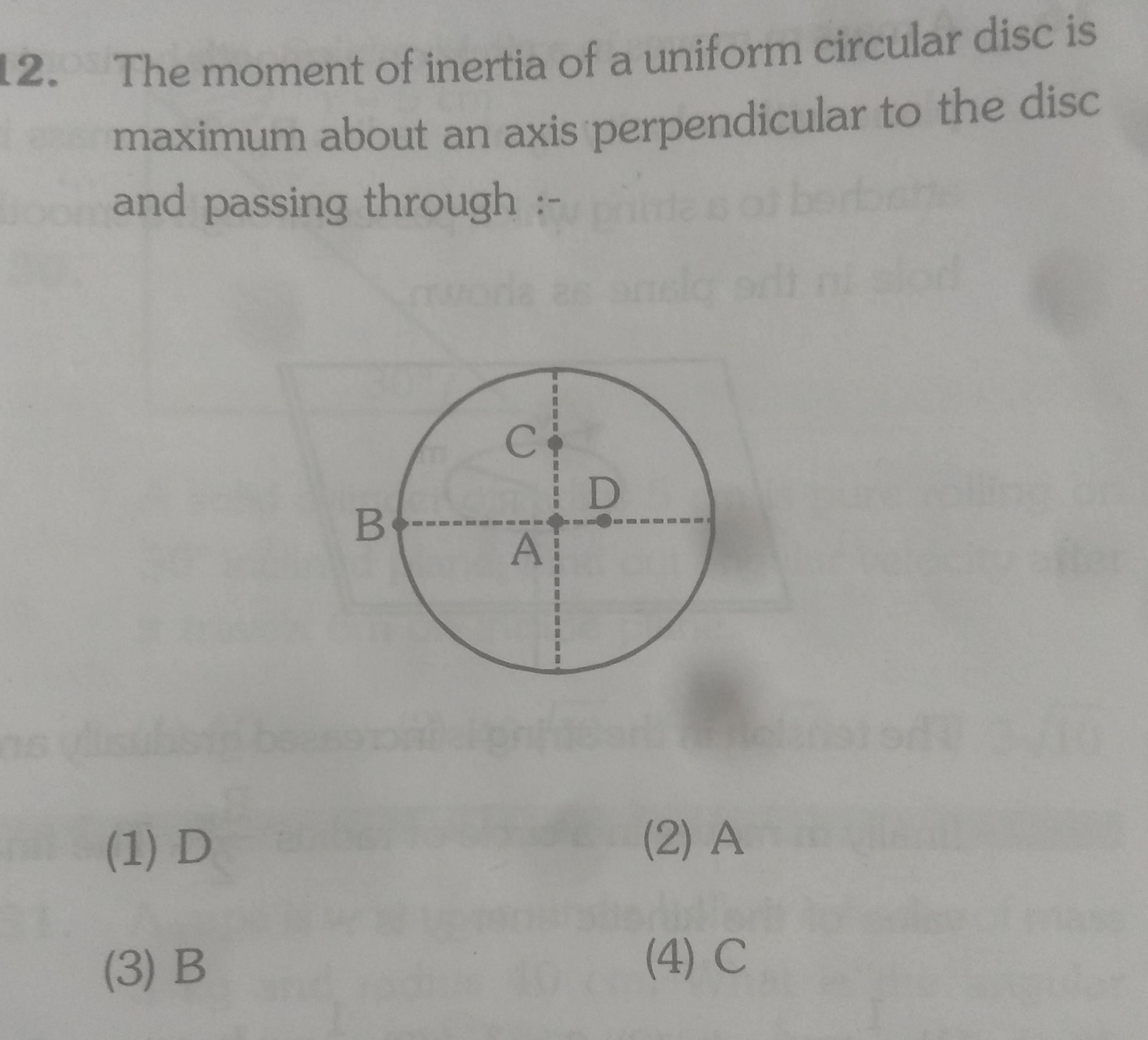
[ANSWERED] 12 The moment of inertia of a uniform circular disc Physics

Example \(\PageIndex{1}\): Moment of Inertia of a Uniform Disk. A thin uniform disk of mass \(M\) and radius \(R\) is mounted on an axle passing through the center of the disk, perpendicular to the plane of the disk. Calculate the moment of inertia about an axis that passes perpendicular to the disk through the center of mass of the disk. Solution


Determine The Moment Of Inertia Of A Plane Circular Disc (i) About An Axis Through Its Centre

However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows; 1. Solid disk


Moment of Inertia of a Disk with a Hole YouTube

The moment of inertia of the rod is simply 1 3 m r L 2 1 3 m r L 2, but we have to use the parallel-axis theorem to find the moment of inertia of the disk about the axis shown. The moment of inertia of the disk about its center is 1 2 m d R 2 1 2 m d R 2 and we apply the parallel-axis theorem I parallel-axis = I center of mass + m d 2 I parallel-axis = I center of mass + m d 2 to find


The moment of inertia of a uniform circular disc about its diameter is 200 gm × cm^2 . Then its

We can also calculate the moment of inertia of a circular disc under different scenarios. These scenarios include; 1. Solid disc. In this scenario, the axis of rotation aligns with the disc's central axis. This is represented as; 2. Axis at the Rim. In this specific case, the solid disc's axis of rotation is positioned at the rim.


How to derive the moment of inertia of a disk YouTube

I parallel-axis = 1 2 m d R 2 + m d ( L + R) 2. Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted axis of rotation, we find the moment of inertia for the compound object to be. I total = 1 3mrL2 + 1 2mdR2 +md(L+R)2. I total = 1 3 m r L 2 + 1 2 m d R 2 + m d ( L + R) 2.


Determine The Moment Of Inertia Of A Plane Circular Disc (i) About An Axis Through Its Centre

actually a ring), then the moment of inertia would be mR2 . The moment of inertia of the disc is actually only half as big as this, because the rings nearer to the center contribute less than they would if they were right at the edge. Example illustrating dependence of moment of inertia on the point of rotation


PPT Rotational Motion PowerPoint Presentation, free download ID6187632

Moment of inertia, in physics, quantitative measure of the rotational inertia of a body—i.e., the opposition that the body exhibits to having its speed of rotation about an axis altered by the application of a torque (turning force).. The moment of inertia of the disk in the figure about OQ could be approximated by cutting it into a number.